Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using a regular expression. Note that the "regular expression" features provided with many programming languages are augmented with features that make them capable of recognizing languages that can not be expressed by the formal regular expressions (as formally defined below).
In the Chomsky hierarchy, regular languages are defined to be the languages that are generated by Type-3 grammars (regular grammars). Regular languages are very useful in input parsing and programming language design.
Contents |
Formal definition
The collection of regular languages over an alphabet Σ is defined recursively as follows:
- The empty language Ø is a regular language.
- For each a ∈ Σ (a belongs to Σ), the singleton language {a} is a regular language.
- If A and B are regular languages, then A ∪ B (union), A • B (concatenation), and A* (Kleene star) are regular languages.
- No other languages over Σ are regular.
See regular expression for its syntax and semantics. Note that the above cases are in effect the defining rules of regular expression.
- Examples
All finite languages are regular; in particular the empty string language {ε} = Ø* is regular. Other typical examples include the language consisting of all strings over the alphabet {a, b} which contain an even number of as, or the language consisting of all strings of the form: several as followed by several bs.
A simple example of a language that is not regular is the set of strings 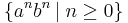 . This is because in this language, the number of a′s controls the number of b′s, which is not allowed by any of the above rules.
. This is because in this language, the number of a′s controls the number of b′s, which is not allowed by any of the above rules.
Equivalence to other formalisms
A regular language satisfies the following equivalent properties:
- it can be accepted by a (nondeterministic) finite automaton, but also by the restricted deterministic finite automaton, or the more general alternating finite automaton
- it can be generated by a regular grammar
- it can be generated by a prefix grammar
- it can be accepted by a read-only Turing machine
- it can be defined in monadic second-order logic
- it is recognized by some finitely generated monoid, meaning it is the preimage of a subset of a finite monoid under a homomorphism from the free monoid on its alphabet
The above properties are sometimes used as alternative definition of regular languages.
Complexity results
In computational complexity theory, the complexity class of all regular languages is sometimes referred to as REGULAR or REG and equals DSPACE(O(1)), the decision problems that can be solved in constant space (the space used is independent of the input size). REGULAR ≠ AC0, since it (trivially) contains the parity problem of determining whether the number of 1 bits in the input is even or odd and this problem is not in AC0.[1] On the other hand, REGULAR does not contain AC0, because the nonregular language of palindromes, or the nonregular language 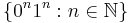 can both be recognized in AC0.[2]
can both be recognized in AC0.[2]
If a language is not regular, it requires a machine with at least Ω(log log n) space to recognize (where n is the input size).[3] In other words, DSPACE(o(log log n)) equals the class of regular languages. In practice, most nonregular problems are solved by machines taking at least logarithmic space.
Closure properties
The regular languages are closed under the various operations, that is, if the languages K and L are regular, so is the result of the following operations:
- the set theoretic Boolean operations: union
 , intersection
, intersection  , and complement
, and complement 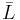 . From this also difference
. From this also difference 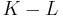 follows.
follows. - the regular operations: union
 , concatenation
, concatenation 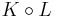 , and Kleene star
, and Kleene star 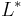 .
. - the trio operations: string homomorphism, inverse string homomorphism, and intersection with regular languages. As a consequence they are closed under arbitrary finite state transductions, like quotient
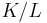 with a regular language. Even more, regular languages are closed under quotients with arbitrary languages: If L is regular then L/K is regular for any K.
with a regular language. Even more, regular languages are closed under quotients with arbitrary languages: If L is regular then L/K is regular for any K. - the reverse (or mirror image)
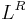 .
.
Deciding whether a language is regular
To locate the regular languages in the Chomsky hierarchy, one notices that every regular language is context-free. The converse is not true: for example the language consisting of all strings having the same number of a's as b's is context-free but not regular. To prove that a language such as this is not regular, one uses the Myhill–Nerode theorem or the pumping lemma.
There are two purely algebraic approaches to define regular languages. If:
- Σ is a finite alphabet,
- Σ* denotes the free monoid over Σ consisting of all strings over Σ,
- f : Σ* → M is a monoid homomorphism where M is a finite monoid,
- S is a subset of M
then the set 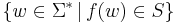 is regular. Every regular language arises in this fashion.
is regular. Every regular language arises in this fashion.
If L is any subset of Σ*, one defines an equivalence relation ~ (called the syntactic relation) on Σ* as follows: u ~ v is defined to mean
- uw ∈ L if and only if vw ∈ L for all w ∈ Σ*
The language L is regular if and only if the number of equivalence classes of ~ is finite (A proof of this is provided in the article on the syntactic monoid). When a language is regular, then the number of equivalence classes is equal to the number of states of the minimal deterministic finite automaton accepting L.
A similar set of statements can be formulated for a monoid 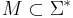 . In this case, equivalence over M leads to the concept of a recognizable language.
. In this case, equivalence over M leads to the concept of a recognizable language.
Finite languages
A specific subset within the class of regular languages is the finite languages – those containing only a finite number of words. These are regular languages, as one can create a regular expression that is the union of every word in the language.
The number of words in a regular language
For any regular language  there exist constants
there exist constants  and polynomials
and polynomials  such that for every
such that for every  the number
the number 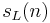 of words of length
of words of length  in
in  satisfies the equation
satisfies the equation 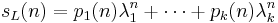 . Thus, a non-regularity of some language
. Thus, a non-regularity of some language 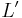 can be proved by counting the words in
can be proved by counting the words in 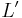 . Consider, for example, the Dyck language of strings of balanced parentheses. The number of words of length
. Consider, for example, the Dyck language of strings of balanced parentheses. The number of words of length 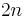 in the Dyck language is equal to the Catalan number
in the Dyck language is equal to the Catalan number 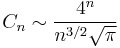 , which is not of the form
, which is not of the form 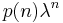 , witnessing the non-regularity of the Dyck language.
, witnessing the non-regularity of the Dyck language.
See also
References
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Chapter 1: Regular Languages, pp.31–90. Subsection "Decidable Problems Concerning Regular Languages" of section 4.1: Decidable Languages, pp.152–155.
- ^ M. Furst, J. B. Saxe, and M. Sipser. Parity, circuits, and the polynomial-time hierarchy. Math. Systems Theory, 17:13–27, 1984.
- ^ Cook, Stephen; Nguyen, Phuong (2010). Logical foundations of proof complexity (1. publ. ed.). Ithaca, NY: Association for Symbolic Logic. pp. 75. ISBN 052151729X.
- ^ J. Hartmanis, P. L. Lewis II, and R. E. Stearns. Hierarchies of memory-limited computations. Proceedings of the 6th Annual IEEE Symposium on Switching Circuit Theory and Logic Design, pp. 179–190. 1965.
External links
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||